|
Масштабы Вселенном столь велики, что по сравнению с ними кажутся крохотными даже первые найденные расстояния до ближайших галактик, вроде галактики Андромеды. Когда впервые было определено расстояние до галактики Андромеды и в моду вошли выражения вроде «сотни тысяч световых лет», считалось, что это почти превосходит человеческое воображение. Однако через десять лет стало очевидно, что Андромеда расположена совсем рядом с нами. Как я уже говорил, она входит в Местную Группу и является членом той же си стемы, что и мы.
И снова встает вопрос где же конец? Все снова и снова человеку приходится расширять свои представления, учиться воспринимать все большие и большие масштабы. Маленькие несветящиеся тела группируются вокруг звезды, образуя планетную систему. Звезды группируются, образуя простые кратные системы, или еще большие рассеянные скопления, или даже еще большие шаровые скопления и галактики, даже еще большие, чем эти последние Галактики объединяются в группы галактик. Не объединяются ли и эти последние в скопления галактик? Вокулер полагает, что это именно так и что, судя по некоторым признакам, существует Сверхгалактика, в которую наша Местная Группа входит как ничтожная ее часть. Если его выводы верны, то мы находимся в десятках миллионов световых лет от центра такой Сверхгалактики, а за ее пределами во всех направлениях расположены другие сверхгалактики.
А не могут ли существовать и скопления сверхгалактик, и скопления скоплении сверхгалактик, и т. д.? Где находится конец? И есть ли вообще конец? Может быть, перед нами простирается безграничная Вселенная?
Если принять эйнштейновскую теорию относительности, то его риманова Вселенная должна иметь конечный объем. Даже если она расширяется, этот конечный объем, непрерывно увеличиваясь, все же остается конечным. 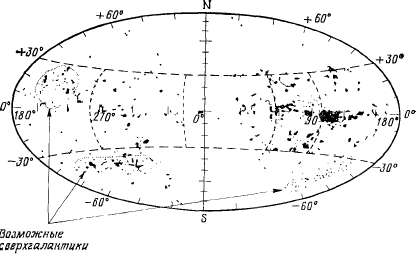
Рис. Сверхгалактики
Иногда выдвигается предположение, что, даже обладая конечным объемом, Вселенная может тем не менее включать в себя бесконечное число галактик. Если это так, то система скоплений скоплений скоплений (и т. д.) галактик может усложняться все больше и больше — до бесконечности.
Но принимая возможность существования бесконечного числа галактик, не столкнемся ли мы вновь с парадоксом Ольберса? Если число галактик во всех направлениях бесконечно, то не будут ли они посылать Земле бесконечное количество света? А раз Земля не получает бесконечного количества света, то не значит ли это, что число галактик конечно?
Если бы риманова Вселенная была статичной, как сперва предположил Эйнштейн, мы должны были бы считать число галактик конечным. Для такой статичной Вселенной довод, который я приведу ниже в доказательство возможности существования бесконечного числа галактик, окажется несостоятельным. В такой Вселенной и объем, и число галактик по необходимости должны быть ограничены и парадокс Ольберса не создает никаких трудностей.
Однако мы, по-видимому, живем в расширяющейся Вселенной, а для такой Вселенной оказывается вполне в силе довод в пользу бесконечного числа галактик. Но как же тогда быть? Каким способом можем мы обойти парадокс Ольберса?
В расширяющейся Вселенной, где все галактики непрерывно удаляются друг от друга, вступает в действие совершенно новый фактор, который нельзя не учитывать. Его не существовало бы, если бы Вселенная была статичной и расстояния между галактиками в среднем оставались бы неизменными. Этот новый фактор -красное смещение.
В расширяющейся Вселенной свет галактик «стареет» и ослабевает. Чем дальше от нас галактика, тем сильнее красное смещение и тем больше ослабление достигающей нас суммарной энергии ее излучения.
А раз излучение, приходящее к нам со все больших и больших расстояний, становится все слабее и слабее, то общая сумма излучения, достигающего Земли, должна быть конечной и притом не очень большой, даже если число галактик бесконечно. Если Вселенная расширяется, то парадокс Ольберса уже не противоречит существованию в ней бесконечного числа галактик.
Это может показаться невозможным. Вы можете подумать, что если каждая из бесчисленных галактик дает хотя бы ничтожное излучение, то, как бы мало оно ни было, суммарное излучение должно оказаться бесконечным. Это предположение иначе можно выразить так: сумма бесконечного ряда чисел, как бы малы ни были отдельные числа, должна быть бесконечной.
Звучит как будто логично, но тем не менее такое рассуждение ошибочно, и это нетрудно доказать. Рассмотрим следующий ряд чисел 1, 1/2, 1/4, 1/8, 1/16. 1/32, 1/64,.. Каждое число равно половине предыдущею, а число членов этого ряда бесконечно. Как бы далеко он ни простирался, его всегда можно удлинить, прибавив половину последнего из написанных чисел, а затем половину этой половины, половину последней половины и так далее до бесконечности.
Может показаться, что сумма такого бесконечного ряда чисел должна быть бесконечной, но попробуйте сложить их. Первое число равно 1, сумма двух первых чисел составляет 1 1/2, сумма первых трех 13/4, сумма первых четырех 17/8. Продолжая сложение, вы скоро убедитесь, что, хотя по мере прибавления новых членов сумма непрерывно увеличивается, она никогда не достигнет 2. Она все более и более приближается к 2, по так и не достигает этой цифры. Итак, сумма ряда 1+1/2 + 1/4+ стремится к 2. Это пример сходящегося ряда, т.е. ряда с бесконечным количеством членов, но конечной суммой.
Излагая парадокс Ольберса в первый раз, я указывал, что в бесконечной Вселенной того типа, о каком говорил Ольберс, каждый слой пространства дает Земле равное количество света. Если свет одного слоя принять за 1, то свет всех слоев будет равен 1 + 1 + 1 +... и так далее до бесконечности. Это расходящийся ряд, и его сумма, несомненно, бесконечна. Именно бесконечность этой суммы и составляет соль парадокса.
Однако с учетом красного смещения каждый слой, лежащий дальше от нас, будет давать меньше света, чем предыдущий.
Если составить такой ряд, он оказывается сходящимся и сумма его конечна. Поэтому во Вселенной Эйнштейна— Римана (все равно статичной или расширяющейся) мы можем забыть о парадоксе Ольберса. Он ничему не мешает.
Но тут возникает новая проблема. Если мы будем учитывать красное смещение, а следовательно, и все большее ослабление энергии достигающего нас излучения все более далеких галактик, нам придется задать вопрос не о том, как велика Вселенная, а о том, какую ее часть мы можем наблюдать. Человек считал бесспорным, что, совершенствуя свои инструменты и улучшая методы, создавая еще более мощные телескопы, еще более точные спектрографы, еще более чувствительные фотопластинки, он сможет заглядывать все дальше и дальше в пространство. Но так ли это? Если излучение далеких галактик становится все слабее и слабее, то не ослабеет ли оно в конце концов настолько, что никакой, даже самый совершенный инструмент уже не сможет его уловить?
Если это так, то размеры Вселенной, которую мы молем наблюдать, принципиально конечны: существует какая-то внешняя граница, заглянуть за которую для нас невозможно. Эта граница охватывает то, что можно назвать наблюдаемой Вселенной.
Для того чтобы узнать, существует ли в действительности такой непреодолимый предел и как далеко он может находиться, нам следует вернуться к закону Хаббла.
|


